Phần 1 : Đệ quy là gì?

31 May 2019

Reading time ~6 minutes

Chào các bạn, do dạo này mình hơi chán nên mình sẽ viết bài hướng dẫn cho các bạn cho đỡ buồn :< Nào let’s start!

1. Khái niệm về đệ quy

In order to understand recursion, one must first understand recursion.

Khái niệm đệ quy đối với một lập trình viên ban đầu rất khó hiểu, vì thế ta hãy xét một vài ví dụ cụ thể trước khi đi vào khái niệm hoàn chỉnh của nó!

Giả sử bạn đi đến phòng ngủ để thay quần áo, nhanh chóng để đi làm cho kịp giờ. Nhưng bạn thấy phòng bị khóa, và bạn biết rằng con trai 3 tuổi của mình giấu chúng trong một chiếc hộp. Mở hộp ra, bạn thấy nó bao gồm nhiều chiếc hộp con khác nữa mà bên trong chúng gồm nhiều chiếc hộp nhỏ hơn. Bạn bối rối và cần tìm cách giải quyết nhanh chóng để không bị muộn làm

Ví dụ

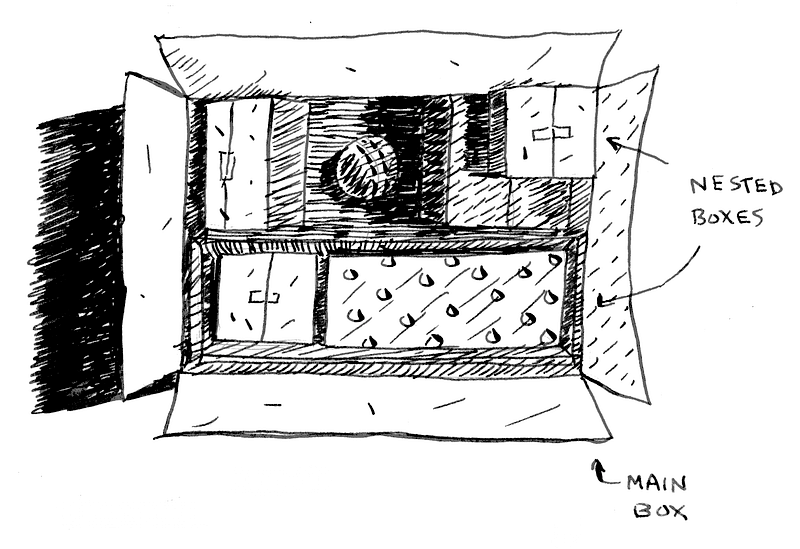
Muốn xử lý vấn đề này, ta có 2 cách tiếp cận : “lặp” (loop) và “đệ quy” (recursion) để tạo nên một thuật toán.

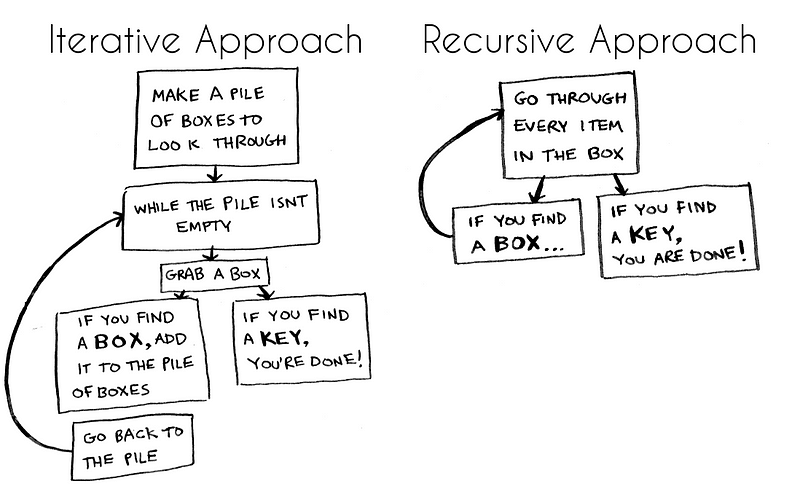
Lặp và đệ quy

Ở cách tiếp cận thứ nhất ta sử dụng một vòng lặp. Cho đến khi không còn chiếc hộp, bạn sẽ lấy ra 1 chiếc hộp từ đống hộp và mở nó ra.
- Trường hợp 1 : Nếu bạn tìm thấy chìa khóa :v Xin chúc mừng bạn đã thành công!
- Trường hợp 2 : Nhưng nếu xui xẻo, bạn lại tìm thấy những chiếc hộp khác, hãy đặt vào đống hộp và làm tương tự!

Mình sẽ minh hoạt bằng mã giả C++ như sau, sử dụng một hàng đợi để lưu đống hộp:

void look_for_key()
{
    bool ok = false;
    queue < box > pile;
    pile.push(main_box);
    while(!pile.empty())
    {
        box this = pile.front();
        pile.pop();
        for(item_in_this)
            if(is_a_key(item))ok =true,break;
            else // item is a box
                q.push(item);
        if(ok)  break;
    }
}

Cách tiếp cận thứ hai, chúng ta sẽ sử dụng đệ quy. Luôn nhớ rằng đệ quy là một hàm gọi lại chính nó.

// init ok = false;
void look_for_key(box)
{
    if(ok)
        break;
    for(item_in_this)
        if(is_a_key(item))
            ok =true, break;
        else // item is a box
            look_for_key(item);
}

Phân tích : Ta thấy rằng ta sẽ mở chiếc hộp ra, nếu tìm thấy chìa khóa, tất nhiên là hoàn thành! Còn nếu thấy chiếc hộp, ta sẽ thực hiện lại các thao tác y như lúc ta mở chiếc hộp ban đầu!

Qua ví dụ trên, phần nào các bạn đã có thể hình dung ra đệ quy là gì!

Đệ quy là phương pháp sử dụng trong chương trình máy tính trong đó sử dụng một hàm gọi lại chính nó.

Ví dụ về đệ quy

2. Cơ chế đệ quy trong tin học

Ví dụ trên có thể khiến bạn nghĩ đệ quy khó hiểu, không đơn giản và làm bạn nản :< Hãy cố gắng lên vì rất nhiều thuật toán sử dụng đệ quy trong tin học. Chúng ta sẽ xét cách hoạt động của đệ quy, đó là cơ chế stack khi gọi các hàm

“Trong khoa học máy tính, một ngăn xếp (còn gọi là bộ xếp chồng, tiếng Anh: stack) là một cấu trúc dữ liệu trừu tượng hoạt động theo nguyên lý “vào sau ra trước” (Last In First Out (LIFO)” - Wikipedia.

Đệ quy thường sử dụng cơ chế stack LIFO - vào sau ra trước khi thực hiện gọi các hàm.
Khi một hàm đệ quy được gọi sau, nó sẽ đặt vào đầu ngăn xếp. Tưởng tượng bạn có một chồng sách, khi đặt lên hay bỏ ra một cuốn sách, bạn luôn ưu tiên cuốn sách trên cùng.

stack

Cùng xét một ví dụ cụ thể liên quan đến toán học, tính giai thừa!

Chúng ra cũng có 2 cách tiếp cận, duyệt và đệ quy, nhưng ở đây ta chỉ xét đến các tiếp cận về đệ quy! Tôi sẽ chỉ cho bạn cơ chế hoạt động của stack trong hàm gọi đệ quy! Đầu tiên, tôi sẽ viết hàm đệ quy tính giai thừa của 1 số!

VD: Giai thừa của 5 sẽ được tính như sau factorial (5) = 5 * 4 * 3 * 2 * 1 = 5!

int fact(int x) // factorial
{
    if(x==1) return 1;
    return fact(x-1)*x;
}

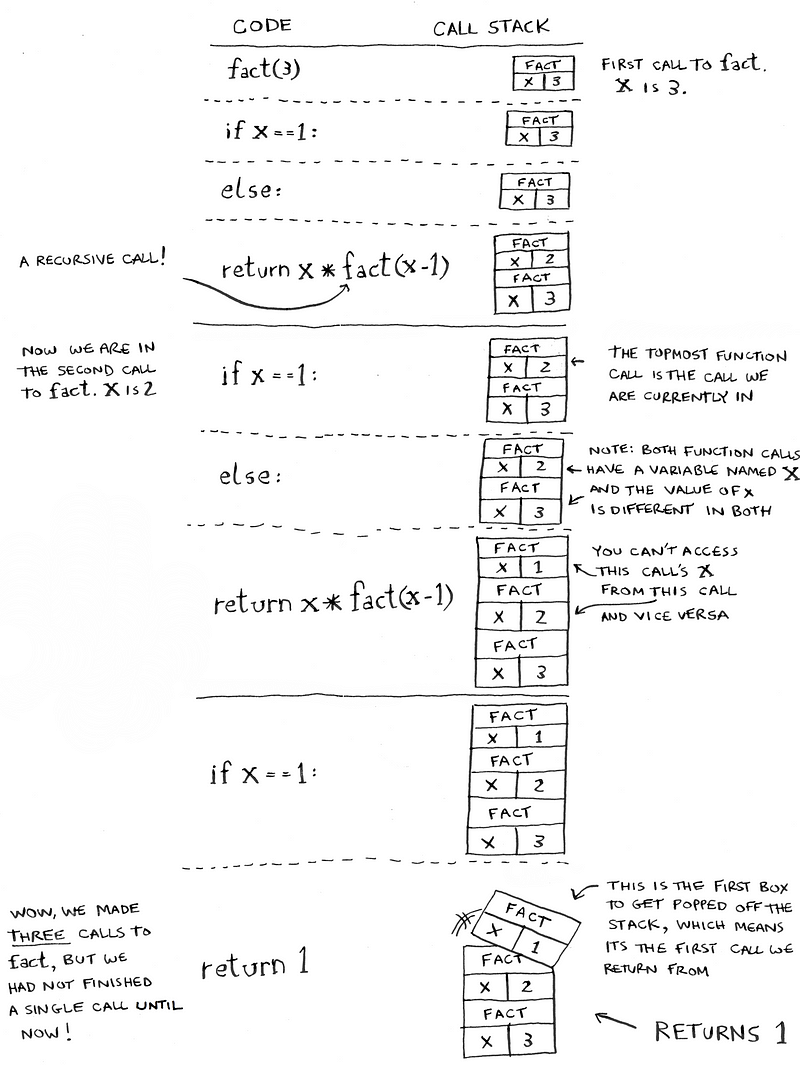
Nào giờ hãy cùng xem điều gì xảy ra khi gọi hàm tính giai thừa của 3 fact(3):

Giải thích :
- fact(3) -> hàm kiểm tra x có bằng 1 hay không, nhưng ở đây x = 3 nên biểu thức logic x == 1 sẽ có kết quả là false. Khi này, hàm sẽ gọi hàm fact(x-1) nghĩa là fact(2)
- Lúc này, hàm được gọi fact(2) sẽ được đặt lên đầu stack. Ta tiếp tục thực hiện.
- fact(2) -> cũng tương tự như fact(3), hàm kiểm tra x có bằng 1 hay không, nhưng ở đây x = 2 nên hàm sẽ gọi hàm fact(1) và đặt vào stack fact(1)
- fact(1)-> hàm kiếm tra đúng bằng 1, nên kết quả sẽ trả về 1. Khi này stack gồm 3 hàm, lấy ra hàm fact(1) đã nhét vào khi trước.
- Tiếp tục lấy ra hàm fact(2), kết quả là fact(2) = fact(1) * 2 = 2!
- Cuối cùng lấy ra hàm fact(3), ta thu được fact(3) = fact(2) * 3 = 3!
Nhận xét : Trong hàm đệ quy luôn có điều kiện tạo nên điểm dừng cho đệ quy. Nếu không có điểm dừng, đệ quy như vong lặp vô hạn vậy!

Bạn đã tìm thấy chìa khóa chưa?

Quay trở lại vấn đề đầu tiên về cách tìm chiếc chìa khóa. Ta nhớ lại rằng phương pháp đầu tiên là duyệt dựa vào đống hộp.

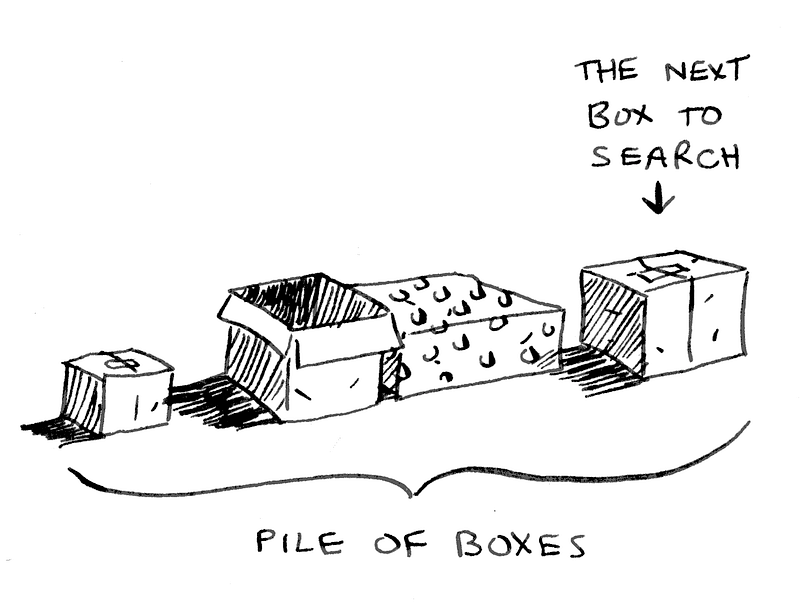
problem first

Ta chú ý rằng đối với đệ quy thì ta không có đống hộp. Thực tế, với cách tiếp cận đệ quy, đống hộp chính là stack lưu các hàm gọi!
Và cám ơn đệ quy, cuối cùng ta đã đã tìm thấy chìa khóa và mở được phòng!

end

3. Ứng dụng đệ quy vào các thuật toán cụ thể!

“Ngày đầu tiên tôi bước vào lớp, tôi bị sốc. Bạn tôi đố nhau về toán học và tin học. Đi đâu tôi cũng nghe cái từ “lệ quy”. Bài nào cũng giải được bằng “lệ quy”. Tôi thấy cái từ này sao nó hay, nó đẹp thế. Mãi sau này tôi mới biết là tôi nghe nhầm từ “đệ quy”.”- trích Tôi đã học tin học như thế nào? - VNOI

Đệ quy được sử dụng trong hầu hết nhiều thuật toán quan trọng và các cấu trúc dữ liệu như Segment Tree/Interval Tree, cây BIT, các thuật toán trên đồ thị như BFS, DFS.
Chú ý tới những đặc điểm quan trọng : đó là điều kiện dừng của đệ quy, hãy nhớ thật kĩ, nếu không có điều kiện dừng, bạn sẽ không thể thoát khỏi đệ quy :v.

Ví dụ về đệ quy

Phần tiếp theo mình sẽ hướng dẫn các bạn 1 kĩ thuật phát triển của đệ quy, là nền tảng cho QHĐ - dynamic programing, một kĩ thuật khá phổ biến và giải quyết được nhiều bài toán khó!

Nguồn tham khảo

1. How Recursion Works — explained with flowcharts and a video

2. Recursion - Wikipedia

Nếu bạn đọc xong bài này mà vẫn chưa hiểu đệ quy là gì :> vậy hãy xem phần 2 của mình tại đây nhé!

recursion